The potential energy is
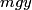 . The x-component of the particle's velocity, expressed in terms of . The x-component of the particle's velocity, expressed in terms of 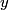 and and 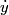 is is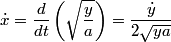 Therefore, the particle's kinetic energy, expressed in terms of 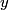 and and 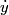 is is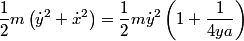 Therefore, the Lagrangian of the particle is 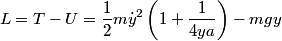 Therefore, answer (A) is correct. |